3 October 2019

By Qiyao Wang
R&D Division, Hitachi America, Ltd.
In today's world, large amounts of repeatedly observed data over time is collected across multiple domains and is being utilized in many different practical applications. Specifically, in the industrial Internet-of-Things (IoT) area, we frequently encounter this type of temporal data, as sensors attached to equipment continuously monitor equipment’s condition and record measurements over time.
When mining useful hidden patterns from such type of data, one of the most fundamental problems of interest is that of temporal covariates predictions. The objective is to build a predictive model that makes predictions for a scalar response variable (can be both Boolean and numerical) given the repeatedly observed covariate variables within a considered time period. An illustrative data example is provided in Fig. 1.
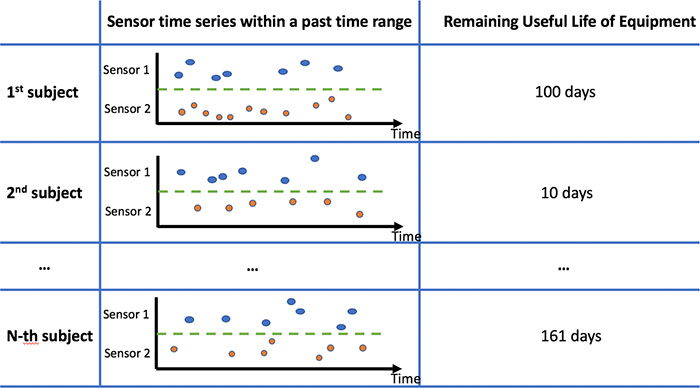
Fig. 1. Problem setting illustration for predictive models with temporal covariates and a scalar response.
This problem is typically solved by the following two existing types of approaches. The first type of approach lies in the traditional multivariate analysis, where the key intuition is to use the raw covariates across different times as the features, to learn the desired mathematical mappings. However, this type of approach is known to suffer from two major limitations:
The second type of approach is the sequential learning model in deep learning, e.g., the Recurrent Neural Network (RNN) and the Long short-term memory networks (LSTM). These models are quite popular for their effectiveness in modeling sequential information in text data and have also been frequently adopted to model time series data. However, these models share certain drawbacks in terms of temporal data modeling:
These concerns can be addressed when the predictive problem is approached from the functional data analysis (FDA) perspective, a branch of statistics that is specialized in modeling continuously and repeatedly observed data over a certain continuum (often time). A comprehensive collection of functional data models can be found in [1]. FDA treats the observed data in Fig.1 as discretized observations of continuous underlying covariate curves over the considered time domain and directly models the curve-type covariates. Given theoretical consistency results for the re-construction of whole curves from discretely observed data under certain smoothness assumptions on the true curves, it is reasonable for FDA models to assume that the entire data curves are assessable. Covariate and response data examples under FDA are given by the last two columns of the table in Fig. 2. The considered predictive modeling problem is , (1) where represents the parameter over time for the -th covariate. The explicit time dimension in covariates and parameters indicates that the sequential information in temporal covariates is well captured and the correlation between the covariates and the response can be different across different times, overcoming limitation in other approaches. Additionally, compared to other approaches that directly model the raw covariates (shown in the second column in Fig. 2), FDA is capable of handling the more flexible type of data, as the entire curves in the functional covariate column are the modeling units. Specifically, the number of observations as well as the observation time locations can be different across different covariates and different subjects.

Fig. 2. Temporal covariates and a scalar response from the functional data analysis perspective.
In FDA, there exists a linear model (Functional Linear Regression [1][3]) and a non-linear model (Functional Neural Network [2]) for the considered predictive model problem in Equation (1). The functional linear regression models can only quantify a simple correlation between the covariates and the scalar response. The Functional Neural Network [2] extends the traditional scalar multilayer perceptron to functional covariate and is capable of recovering more complex relationships between the covariates to the response. However, the proposed network in [2] is valid only for the so-called dense functional data scenarios, where there are a large number of regularly spaced observations for any given covariate of a considered subject. An example of dense functional data is illustrated by the yellow dots in the left panel of Fig.3. Sparse functional data appears in a variety of useful application in the industrial world, where there are only a limited number of possibly irregularly spaced observations available for a given covariate of a considered subject (please see the right panel of Fig.3). Examples include sensor measurements from equipment that was collected using mobile devices (such as hand-held vibration meters), measurements with a significant amount of missing values due to sensor malfunction or communication errors, and measurements from the Internet of Things (IoT) systems with infrequently sampled data to reduce data storage and transfer costs.
Here is the major difference between dense and sparse data. When data is densely observed, it is feasible to recover the underlying curve (the blue curve) using the observed data from this subject alone (the yellow dots). However, when data is sparse, it is no longer reliable to recover the individual curves using the observed data from this subject alone. Borrowing the idea from the functional linear regression for sparse data in [3], we propose a new Functional Neural Network which has been theoretically and experimentally shown to work for both sparse and dense functional data in our paper [4]. (See Fig.4.)
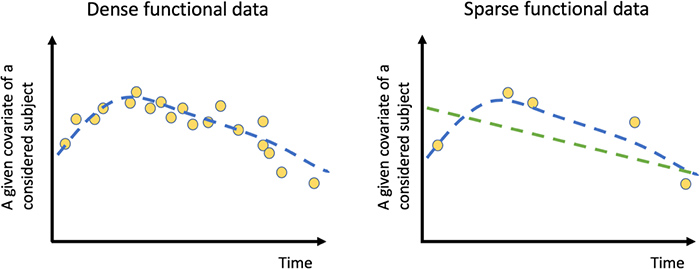
Fig. 3. Dense and sparse functional data.

Fig. 4. Summary of four different functional regression models for the problem in Equation. (1).
The architecture of our proposed functional neural network is summarized in Fig.5. The overall structure is similar to the functional neural network in [2], where an innovative sparse functional neuron has been proposed to handle the sparsity in covariates. (For detailed derivations and the mathematical details of the proposed models please refer to the paper [4]).
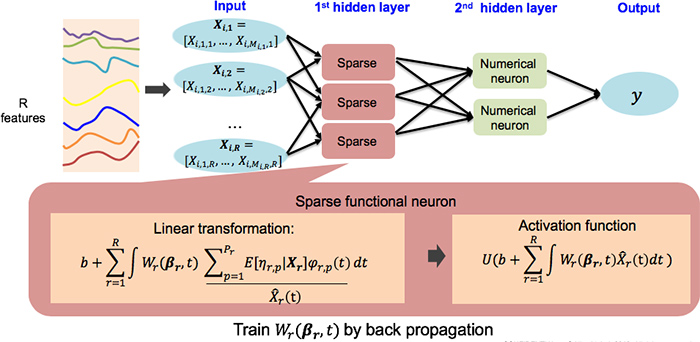
Fig. 5. Architecture of the proposed functional neural network.
The superior performance of our proposed model over the two common practices, i.e., multivariate analysis with the traditional Multilayer Perceptron and LSTM, has been illustrated by several numerical experiments in our paper [4]. In one of the experiments, we consider a fundamental problem of interest to the prognostic and health management community. Given the current and previous sensor readings from an equipment, how to estimate the remaining useful life (RUL) of the equipment, i.e., how much time is left until the equipment reaches its end of life. We consider a widely-used benchmark data set called NASA C-MAPSS (Commercial Modular Aero-Propulsion System Simulation) data for the RUL estimation problem. The data set is a simulated data set without any irregularity and missing values. To mimic real scenarios where there is usually a certain level of irregularity in time series trajectories, we sparsify the data set by randomly keeping a certain percentage of the raw data (30%, 50% or 100%) for each of the engines in the training and testing data. The accuracy metrics summarized in Fig. 6 indicate that:
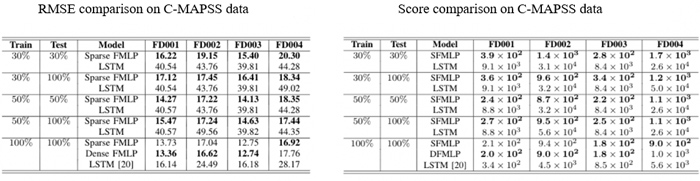
Fig. 6. Accuracy metrics for RUL estimation on the C-MAPSS data set.
Enlarge (Open new window)
We believe that our proposed model is potentially useful in a wide range of applications where the objective is to build a predictive model from timely observed covariates and a scalar response variable of interest. Compared to alternative approaches, our proposed approach has the following advantages when it is reasonable to assume that the underlying covariate curves are smooth:
For more details, we encourage you to read our paper [4].
References