10 September 2020
Ryota Kamoshida
Research & Development Group, Hitachi, Ltd.
Production scheduling is the process of assigning tasks to machines in the manufacturing industry. One common problem in production scheduling is known as the job-shop scheduling problem (JSSP) where multiple jobs are processed on multiple machines. Each job consists of an ordered sequence of tasks and each task is processed on a specific machine. JSSP is known as a difficult problem of finding an optimal schedule and has resulted in numerous studies. In actual factories however, in addition to finding the optimal schedule there is also a need to optimize facility layout, that is the facility layout planning (FLP) of portable machines to appropriate locations where they can be used. JSSP and FLP are both key elements in maximizing the efficiency and productivity of manufacturing systems but to date they have largely been studied independently of each other. This blog is an overview of a method that we are proposing to incorporate dynamic and flexible FLP with job-shop scheduling to efficiently solve FLP-integrated JSSP.
Table 1 describes a simple JSSP with three jobs and six machines. The first operation of job 1 uses machine 1, and its processing time is one. Figure 1 shows an example of a facility layout. In Figure 1 (a), machines 1, 3, and 5 are used at predetermined locations. The numbers in the layout correspond to the respective machine numbers. Machines 2, 4, and 6 are portable machines and are used at the vacant location. The two numbers in Figure 1 (b) indicate the job number and the machine number, e.g., "1-2" means the operation of job 1 uses machine 2. Each square represents the area occupied by the operation.
Table 1: 3×3 job-shop problem
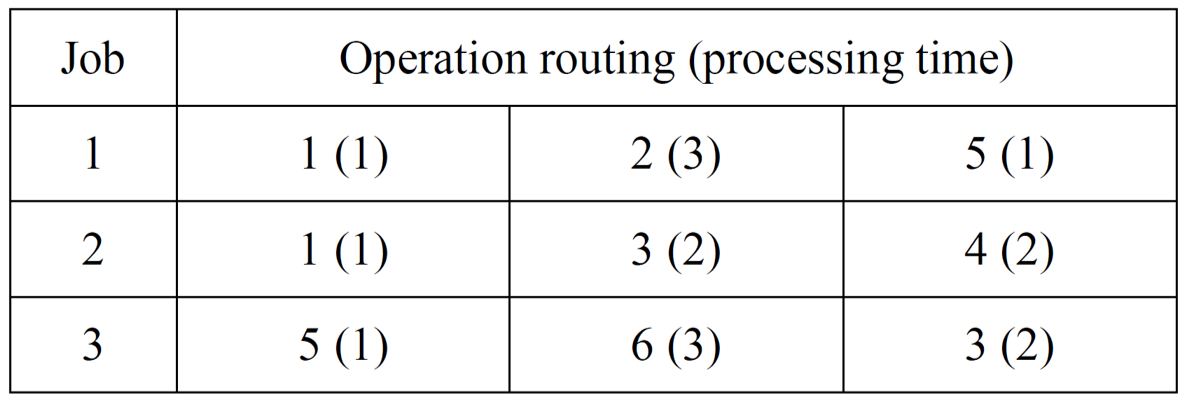
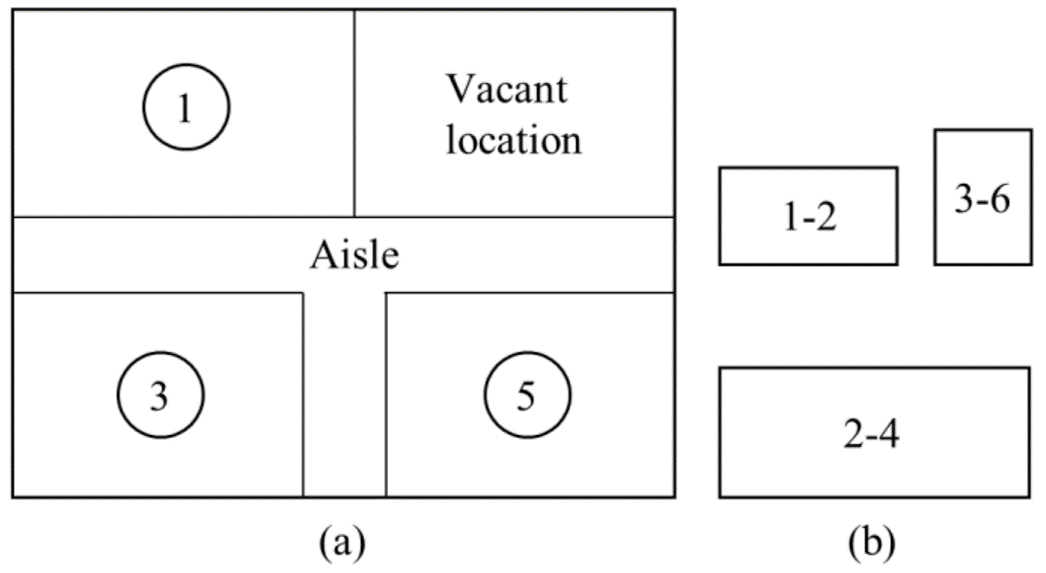
Figure 1: Layout with vacant location
Figure 2 shows how FLP affects the result of JSSP. In Figure 2(a), the result of scheduling without considering FLP is represented as a Gantt chart. The horizontal axis represents time. In this case, the maximum time to complete all jobs (makespan) is six. However, when the FLP problem is considered, operations 2, 4, and 6 cannot be processed at the same time due to the size of the vacant location. Hence, the schedule is modified as shown in Figure 2 (b). The makespan increases from six to seven. An optimal solution, where the makespan is six, is shown in Figure 2 (c). As shown above, the sequential optimization of JSSP and FLP may not result in minimized makespan. We therefore decided to focus on concurrent optimization of JSSP and FLP.
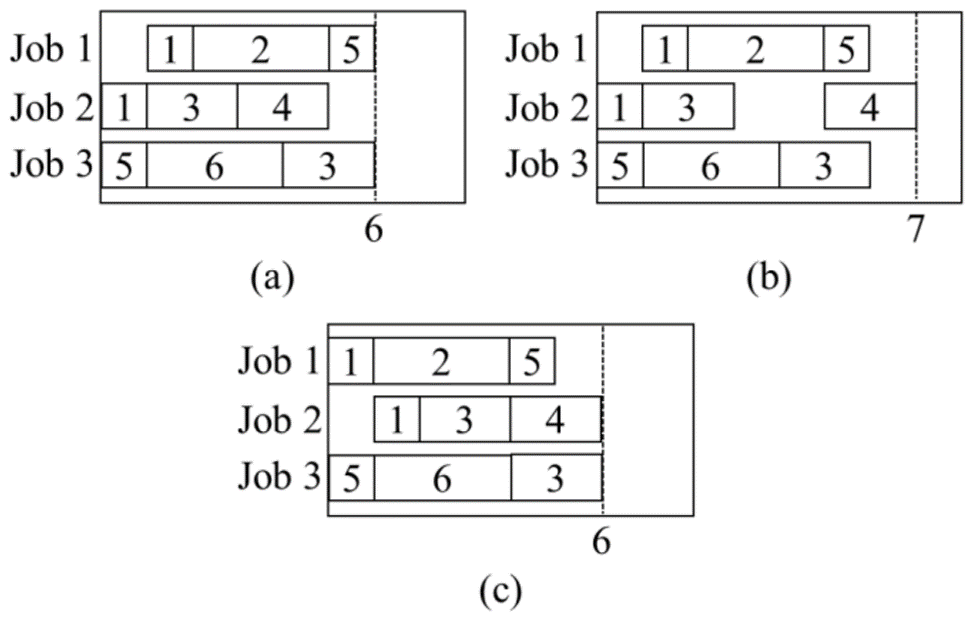
Figure 2: Examples of Gantt chart
The Giffler and Thompson (GT) algorithm [1] is commonly used to obtain a feasible schedule. We modified the GT algorithm to solve JSSP and FLP simultaneously. Figure 3 describes the difference between our method and conventional methods. We formulated FLP as a strip packing problem and solved it by the Best Fit (BF) algorithm [2]. Then, we directly incorporated the BF algorithm into the GT algorithm, which enabled us to solve the problem more efficiently than conventional methods. For more details, we encourage you to read our paper [3].
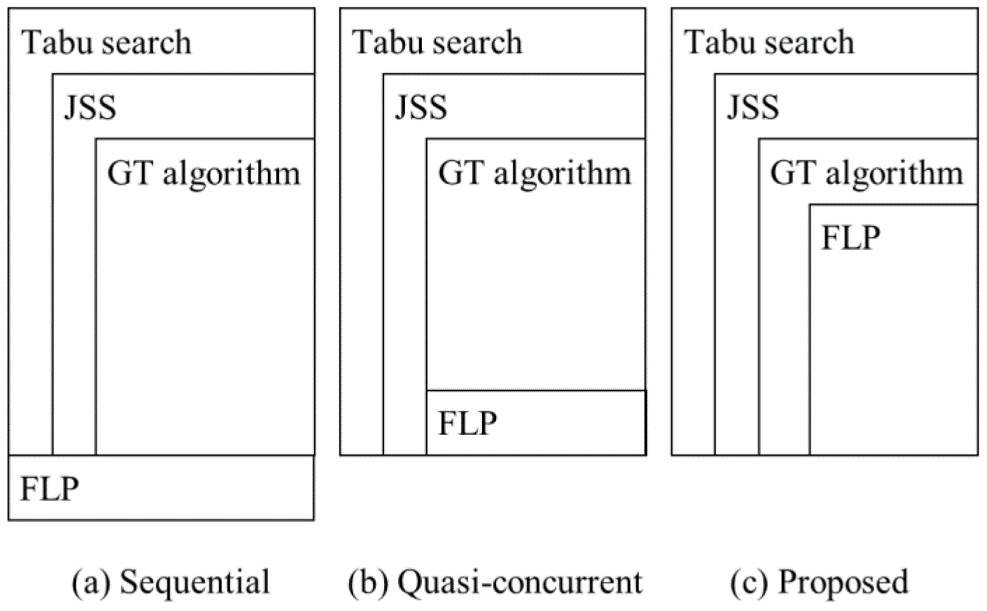
Figure 3: Difference between optimization methods
We evaluated the effectiveness of our method using three datasets (la01, la06, la16) that were made by modifying commonly used benchmark datasets in OR-Library [4]. The results are listed in Table 2. Our method outperformed the conventional methods with all datasets. Figure 4 represents the relationship between the narrowness of the vacant location and makespan. The narrower the area of vacant locations, the more efficiently our method solved the problem.
Table 2: Evaluation results
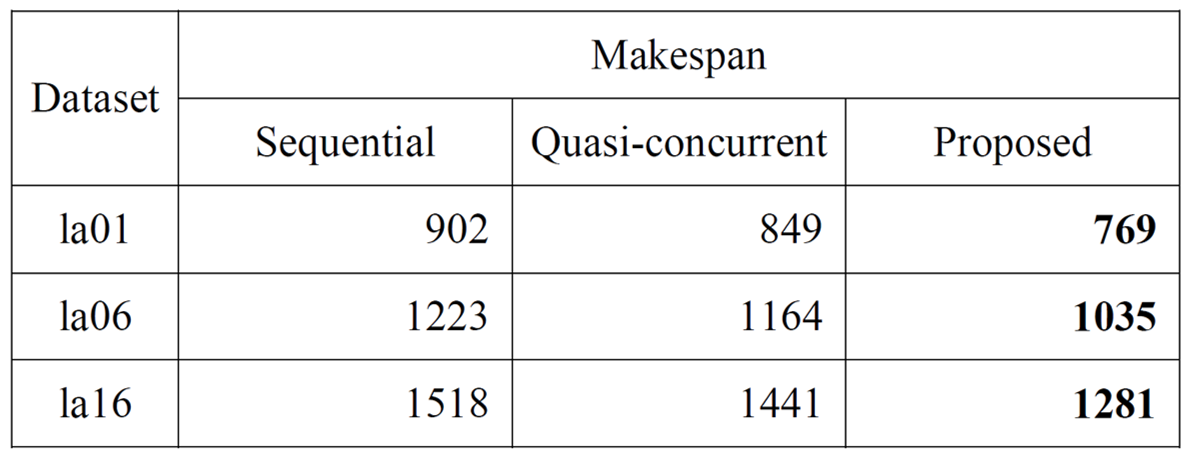
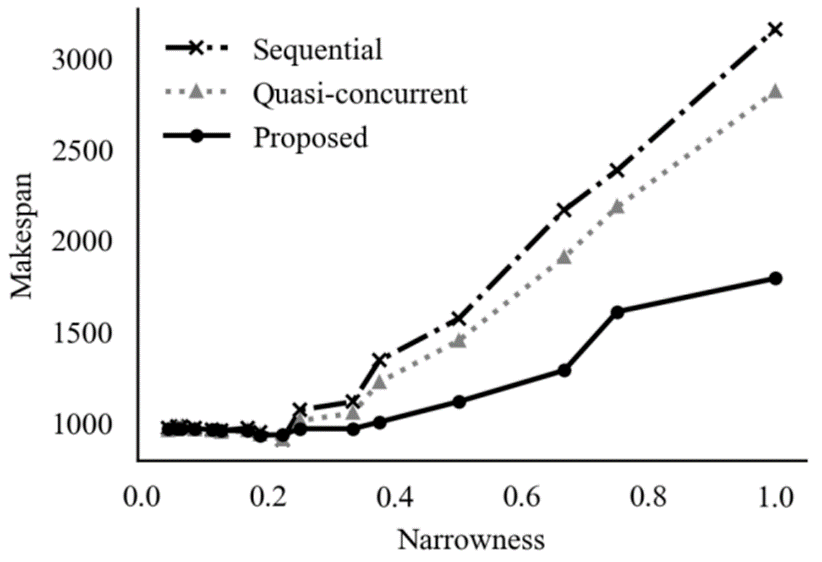
Figure 4: Relationship between narrowness of vacant location and makespan
Our method which concurrently solves JSSP and FLP can make efficient schedules especially in the case with narrower vacant locations. We hope that the outcome our study will be useful in improving the efficiency and productivity of manufacturing systems.