21 January 2022

Ahmed Farahat
R&D Division, Hitachi America, Ltd.
Industrial networks of equipment are the backbone of resilient business operations. They are large-scale systems that consist of several interacting components. For example, water supply networks consist of connected components such as water tanks, pumps and pipes. Failure of any one component may disrupt the entire network, making it non-functional, and result in safety hazards and costly repairs. Thus, it is crucial to continuously monitor and maintain industrial networks to prevent any failure. Traditionally, monitoring such systems are focused on detecting faults on the level of a single component by considering the measurements generated by that component. These solutions are sub-optimal as they are independently applied to individual components without explicitly taking into consideration the dependency between the several components that co-exist in the network. Ignoring the interaction between components makes fault detection much more challenging. A fault in a component (say a leakage in a tank or a pipe) can affect the neighboring components. Therefore, designing a monitoring system without considering the network structure can degrade the diagnosis performance significantly. In order to solve this problem, my team and I looked at first modeling the industrial networks as weighted undirected graphs. The graph structure represents the connected components. We then used graph convolutional neural networks (GCNN) to detect and isolate faulty components in these systems. We applied our proposed method to a case study of a simulated water supply network and showed that GCNN outperforms traditional approaches for leakage detection.
In this work, we present a new solution in which we formulate fault detection and isolation (FDI) in industrial networks as a node classification problem over undirected graph and use GCNN to solve this problem. In our model, each node represents a component. The data at each node represent the measurements associated with the corresponding component. We consider undirected graphs because in industrial networks typically when component A is connected to component B, component B is also connected to component A. The graph structure encodes pairwise relationship between the components; 1) the edges show connection between components, 2) the weight of an edge shows the degree of connection between components. We assume the graph structure (the graph’s edges, and the weight of each edge) are known. In many practical cases, this information can be provided by domain experts. It is also possible to learn the graph structure using operation data.
Most of machine learning (ML) algorithms are developed to operate on a vector space. Graphs represent much more complex data structures. Traditionally, graph embedding methods have been used to transfer graph data to a vector space. For systems with a few nodes and limited connections between higher order neighbors, graph embedding can be a simple solution. However, in general, graph embedding leads to information loss, and extra computational complexity. A more efficient approach is to adapt ML algorithms to the graph domain. Convolutional neural networks (CNNs) use convolutional filters to extract features from images. Similarly, graph CNNs (GCNNs) use graph Fourier transform (GFT) to extract features from graphs.
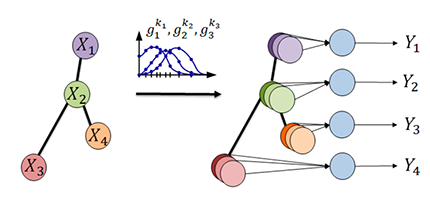
Figure 1. A graph convolutional layer for a graph with 4 nodes (N=4). \(X_n\) represents graph measurements in node n. \(g_l^k\) represents a k-hop graph convolutional filter to be learned. Y represents components labels (normal or faulty)
Figure 1 represents our approach for FDI. Xn represents the signal measurements of component n and is the input to the network. A k-hop graph convolutional layer extracts features using nodes with shortest path distance less than k. The network can have multiple layers for different k-hop degrees to capture different levels of connections between the components. Y is the output of GCNN and represents the vector of node labels which can be normal or faulty. Graph convolutional filters capture the interactions between the components in normal and faulty operations. Learning these features helps GCNN to distinguish normal interaction from fault propagations in the system. Moreover, using the graph convolutional filter reduces the overfitting by restricting the model to learn relationship between k-hop connected components.
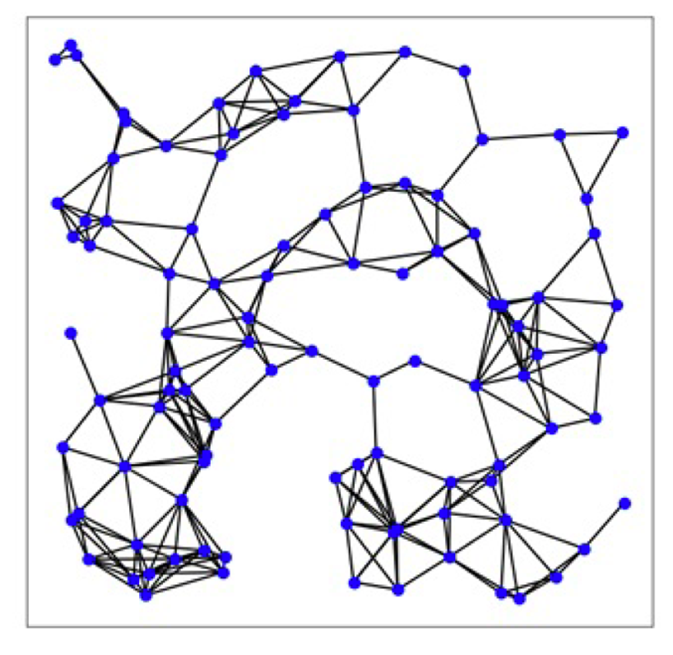
Figure 2. Water tank network: an industrial network with 100 components
To demonstrate the effectiveness of our method, we conducted a case study on a simulated network of 100 connected water tanks. The water system network dataset is available at https://github.com/IndustrialNetwork/GraphDataset. The network as shown in Figure 2 represents a connected graph which means there is a path from any tank to any other tank in the network through the pipelines. This means a fault in a tank will affect the measurements at every other tank in the network. Therefore, using only local measurements for FDI can decrease the detection rates and increase false alarms. Since a fault in a component can affect any other component, it may seem reasonable to use all the tanks measurements for FDI. However, in a system with several components, using all the components measurements can result in overfitting, which can also result in low detection rates and high false alarm rates in the application step. Figure 3 shows the diagnosis performance of GCNNs with different number of layers and different localizations plus few other baseline methods for comparison. It is worth noting that the effect of overfitting is so significant to the extent that univariate SVM which only uses component local measurements performs better than fully connected NNs. It can also be noted that the performance of GCNN can be improved by using different localizations. The proper level of localization depends on the network structure and degree of connection between k-hop neighborhoods. In general, selecting a lower value for k can prevent the network from learning higher order interactions in the graph. On the other hand, selecting a higher value for k can lead to overfitting. We encourage the readers to refer to the original paper for more details [1].
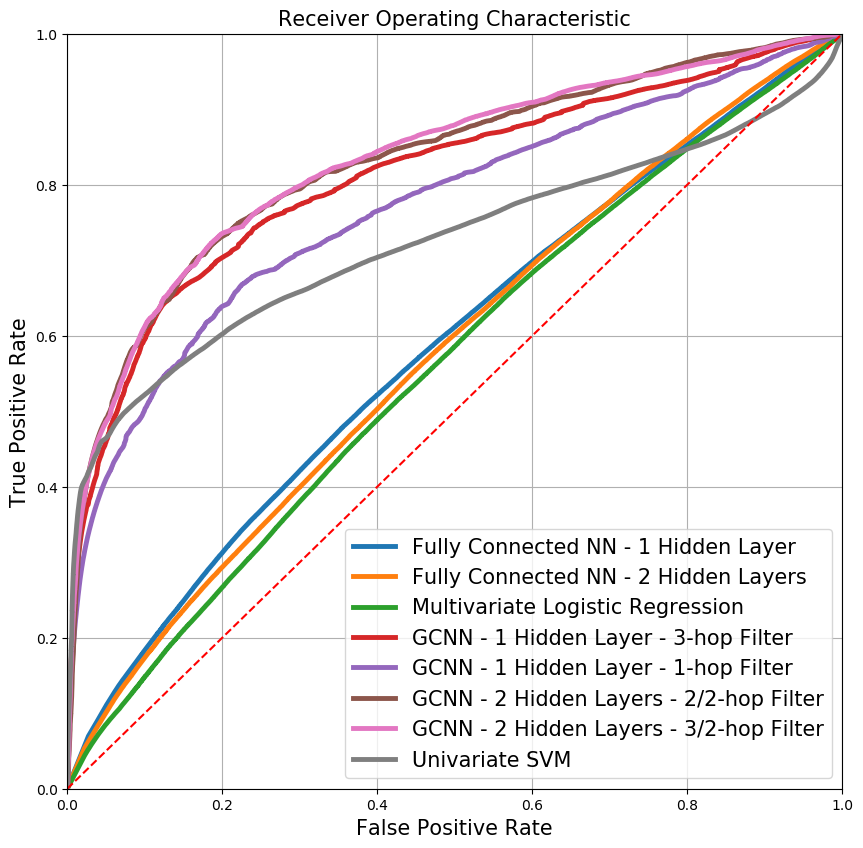
Figure 3. Comparison of different models
In this work, we presented a data-driven method to address FDI in large-scale industrial networks with several interacting components. Applying the method to a simulated water supply network showed that our method significantly outperformed several baseline algorithms in leakage detection as it accommodated for the connections between the numerous components of the network. In the future, we will be looking at how we can apply our method to different industry use cases.
The author would like to thank Hamed Khorasgani for co-authoring this article, and Hamed Khorasgani, Arman Hasanzadeh, and Chetan Gupta for their contribution to this research.