9 October 2020

Takuya Okuyama
Research & Development Group, Hitachi, Ltd.
Optimization is a key advantage offered by digital technology to enhance societal systems. If we are able to solve large-scale optimization problems quickly, this can significantly improve many systems. We worked with the National Institute of Informatics in Japan to develop efficient optimization technology for practical solutions to large-scale optimization problems such as financial portfolio, transportation route search, and shift scheduling optimization problems.
Various techniques have been developed to solve optimization problems efficiently. One particularly well-known technique is the simplex method developed by George Dantzig in 1947 [1]. In the same period, the accumulation of theoretical and electronic technologies related to computer science resulted in the emergence of computers. In the late 20th century, with the development of optimization techniques and devices, optimization problems were solved by executing algorithms on Neumann-type computers.
At the turn of the 21st century, however, a quantum annealing machine designed to solve quadratic unconstrained binary optimization (QUBO) problems was announced [2]. Quantum annealing machines attract much attention because there is an expectation that they will demonstrate an advantage over Neumann-type computers in computational time when solving the optimization problems, as a wide variety of combinatorial optimization problems are known to be convertible to QUBO problems. (See Figure 1 for the computing flow of optimization with QUBO formulation.) One problem though, is that it is difficult to scale up these machines while retaining a quantum nature. Further, a computationally intensive pre-processing run on conventional computers is required before inputting the problem on the quantum device without all-to-all spin connection. As a result, it takes more time overall to obtain the result.
To overcome the above-mentioned challenges faced by annealing machines designed to solve sparsely-connected QUBO problems and to solve large-scale real-world problems, my colleagues and I proposed an optimization algorithm called momentum annealing (MA) [3].
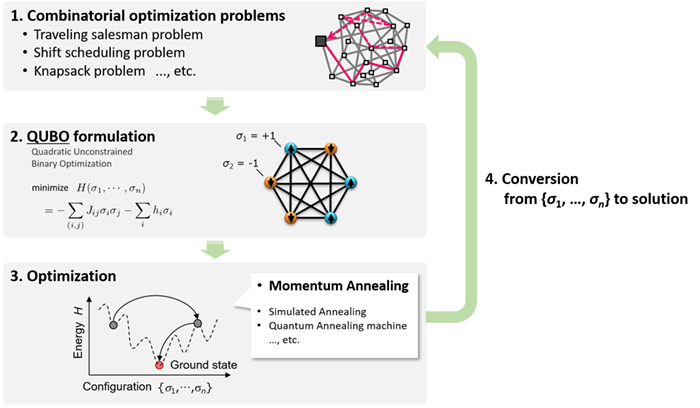
Figure 1: Computing flow of optimization with QUBO formulation
MA is one of several annealing methods. Before explaining MA, I’d like to first briefly describe another annealing method, simulated annealing (SA) [4]. SA is a probabilistic approximate algorithm for finding a state such that a given function f(x) is minimized. It consists of discrete-time Markov processes that converge to a Boltzmann distribution. The existence probability of state x in the distribution is proportional to exp[−f(x)/T], where T is a parameter called temperature. Sampling from the distribution at low temperature attains an optimal or near-optimal solution with high probability. According to the same theory, MA also explores an approximated or the optimal solution. The difference between MA and SA is whether they are allowed to update several variables in parallel theoretically or not.
MA is designed to have affinity with parallel computations and can accelerate the calculation using large-scale parallel processing. We implemented the MA on GPUs (Graphics Processing Units) because its massive parallel computation makes the optimization operation faster. Figure 2 shows the experimental results using MA and SA to solve a randomly generated QUBO problem with 100,000 variables. We ran MA on 4 NVIDIA Tesla P100 connected by NVLink and reported that it took 1/250 of the computational time to reach an approximate solution compared with SA on IBM POWER8.
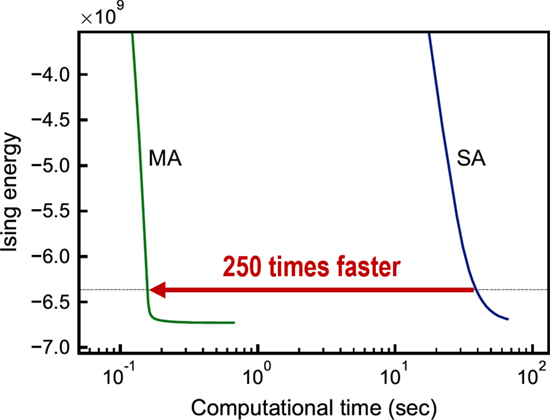
Figure 2: Experimental results obtained with MA (momentum annealing) and SA (simulated annealing) solving a QUBO problem with 100,000 variables. The horizontal axis represents the computation time and the vertical axis represents the objective function value of the problem.
MA does not require computationally intensive pre-processing that is needed in other quantum annealing machines. Furthermore, there is the added advantage of speeding up the computation by being able to use parallel computing. Due to these two key features, our proposed algorithm was able to quickly complete optimization calculations as shown above.
In this post, I described our experiment with MA for a randomly generated problem. As we move toward practical applications, my colleagues and I have started proof of concepts on topics such as insurance portfolio optimization (related release in Japanese) and shift scheduling for COVID-19 infection prevention. It won't be long we believe before we can offer you our latest optimization technology.
For more details, we encourage you to read our paper, “Binary optimization by momentum annealing.”